⚡ Sorting Algorithm Series – Part 2: Selection Sort
Deep research on Selection Sort
Selection Sort: A Step-by-Step Guide
When we first start learning sorting algorithms, Selection Sort is often one of the first we encounter. It’s simple, easy to understand, and a great way to build intuition about how sorting works.
What is Selection Sort?
Selection Sort works by dividing the input list into two parts:
A sorted part (which grows as the algorithm progresses)
An unsorted part (which shrinks as elements are moved into the sorted part)
At each step, the algorithm finds the smallest (or largest) element in the unsorted part and swaps it with the first unsorted element, effectively growing the sorted section by one.
When to Use Selection Sort
✅ Good for:
Small datasets
Scenarios where memory writes are expensive, since Selection Sort minimizes the number of swaps compared to algorithms like Bubble Sort
❌ Not good for:
Large datasets (because of its O(n²) complexity)
Performance-critical applications where faster algorithms like Quicksort or Mergesort are better choices
Time Complexity
Best case: O(n²)
Average case: O(n²)
Worst case: O(n²)
Unlike Bubble Sort, there’s no early exit condition—Selection Sort will always perform roughly the same number of comparisons
Where is Selection Sort Used in Practice?
Selection Sort is rarely used in real-world production systems because it’s inefficient compared to modern algorithms.
However, it still has some value:
In educational contexts (to teach sorting fundamentals)
In memory-constrained environments where minimizing swaps is more important than minimizing comparisons
In cases where writes to memory are costly (e.g., flash memory with limited write cycles)
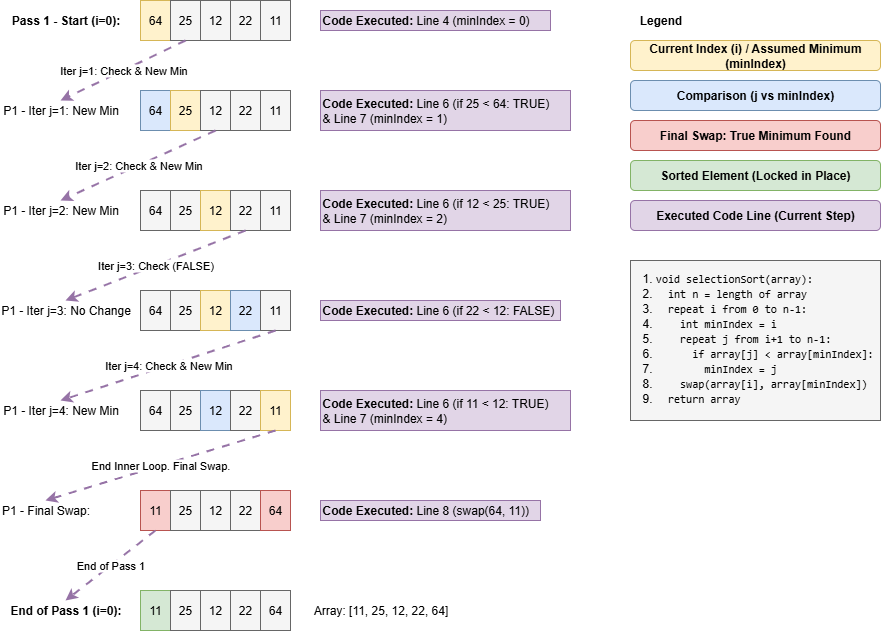
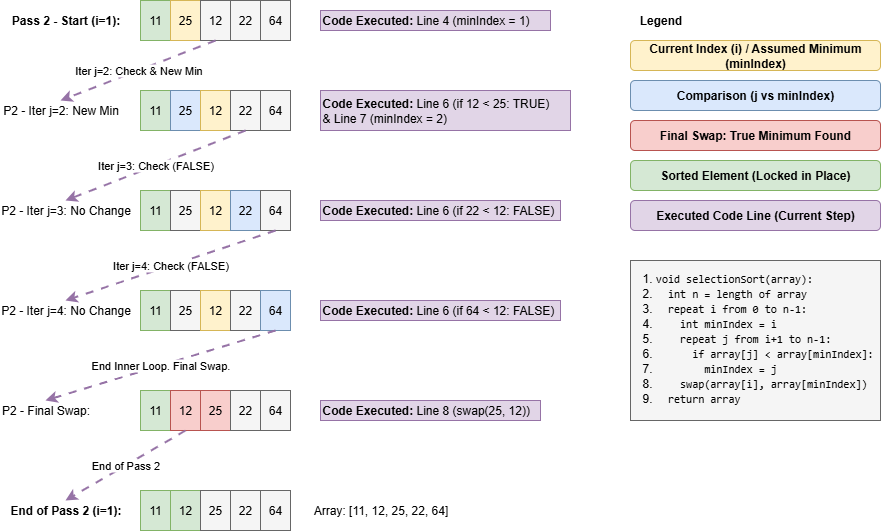
Selection Sort Algorithm (Pseudocode)
void selectionSort(array) {
int n = length of array
repeat i from 0 to n-1 {
int minIndex = i
repeat j from i+1 to n-1 {
if array[j] is lesser than array[minIndex]
minIndex = j
}
swap(array[i], array[minIndex])
}
return array
}Example
Given the array: [64, 25, 12, 22, 11]
Pass 1
Pass 2
Pass 3
Pass 4
Pass 5
Key Takeaways
Selection Sort is simple, intuitive, and a great teaching tool.
It minimizes swaps, making it useful in situations where memory writes are costly.
However, it has O(n²) time complexity, so it’s not suitable for large datasets.
✨ Next up in this sorting series: we’ll explore Insertion Sort, which works better than Selection Sort for partially sorted arrays.
👉 Subscribe (it’s free!) to receive upcoming posts directly in your inbox and support my work.





Thanks for this!
Selection Sort always seemed so simple but I never really understood why anyone would use it over other algorithms. The memory write angle makes total sense now, never thought about flash memory or embedded systems having those constraints.
Can't wait for the Insertion Sort comparison!